強化学習におけるReinforceを5行程度で説明して下さい(江端メモ)

2025年8月31日

強化学習におけるReinforceを5行程度で説明して下さい

Reinforceは、方策勾配法の最も基本的なアルゴリズムである。
エージェントは環境との相互作用からエピソード全体の報酬を得て、その合計報酬を基準に行動確率を更新する。
具体的には「得られた報酬が大きい行動の確率を高め、報酬が小さい行動の確率を下げる」方向にパラメータを勾配上昇させる。
この方法は単純だが、分散が大きく学習が安定しにくい問題がある。
その後のアルゴリズム（Actor-Criticなど）は、この分散を抑える工夫を加えて発展している。

状態S_0 → 行動A_0 → 報酬R_0 → 状態S_1 → 行動A_1 → 報酬R_1 → .... を繰り返すというデータがあったとする。

なるほど、収益は、その後の行動に影響するが、遠い未来は、rで減衰させる、ということだな。

深層学習の関数とは何ですか。簡単に説明して下さい。簡単な例題があればお願いします

深層学習における「関数」とは、入力を受け取り、出力を返す仕組みを数式で表したものを指す。
ニューラルネットワーク全体は「複雑な関数」であり、各層で「単純な関数（線形変換＋非線形変換）」を重ねていくことで成り立っている。
例えば1つの層では、入力ベクトル

x

に対して重み

W

とバイアス

b

を使い、

f(x) = \sigma(Wx + b)

という関数を定義する。ここで

\sigma

は活性化関数（例：ReLUやシグモイド）である。

簡単な例題

入力

x = 2

、重み

w = 3

、バイアス

b = 1

、活性化関数をReLU（負の値を0にする関数）とすると、

f(x) = \text{ReLU}(wx + b) = \text{ReLU}(3 \times 2 + 1) = \text{ReLU}(7) = 7

となる。
このように、深層学習は「多数の関数を組み合わせて、大きな入力（画像や音声など）から目的の出力（分類ラベルなど）を計算する仕組み」と考えられる。

もっと具体的な関数の種類（例えばシグモイド関数やソフトマックス関数）についても例を見たいですか？

シグモイド関数やソフトマックス関数の例を見たいです

了解しました。代表的な「シグモイド関数」と「ソフトマックス関数」を、簡単な数値例で説明します。

1. シグモイド関数 (Sigmoid)

式：

\sigma(x) = \frac{1}{1 + e^{-x}}

入力を 0〜1の範囲に圧縮する関数。確率っぽい値を出すためによく使われる。

例

$x = 0$

\sigma(0) = \frac{1}{1+e^0} = \frac{1}{2} = 0.5

$x = 2$

\sigma(2) \approx \frac{1}{1+e^{-2}} \approx 0.88

$x = -2$

\sigma(-2) \approx 0.12

2. ソフトマックス関数 (Softmax)

式（複数入力

z_1, z_2, ..., z_n

に対して）：

\text{Softmax}(z_i) = \frac{e^{z_i}}{\sum_{j=1}^{n} e^{z_j}}

複数の値を 確率分布（合計1になる） に変換する関数。分類問題の出力層でよく使われる。

例

入力が

[2, 1, 0]

の場合：

$e^2 = 7.39, \; e^1 = 2.72, \; e^0 = 1$
合計 = $7.39 + 2.72 + 1 = 11.11$
Softmaxの出力は：

[\, 7.39/11.11, \; 2.72/11.11, \; 1/11.11 \,] \approx [0.67, \; 0.24, \; 0.09]

つまり、入力

[2,1,0]

を確率分布に変換すると「クラス1が67%の確率で正しい」といった形になる。

Reinforceは、離散時刻tのデータがあるものに用いられる、という理解で良いですか？

はい、その理解でおおむね正しいです。

補足説明

Reinforceは方策勾配法 (policy gradient) の一種で、離散的な「時刻

t

」ごとにエージェントが行動を選び、環境から報酬を受け取る状況を前提にしています。つまり、

状態 $s_t$
方策 $\pi(a_t|s_t)$
報酬 $r_t$

例

例えば「迷路探索」や「強化学習の標準タスク（CartPoleなど）」は、すべて1ステップずつ行動→報酬→次状態、という離散的な流れであり、Reinforceはそのデータを使って方策の更新を行います。

逆に「連続時間」での学習や制御にも拡張は可能ですが、その場合は一度離散化して扱うのが一般的です。

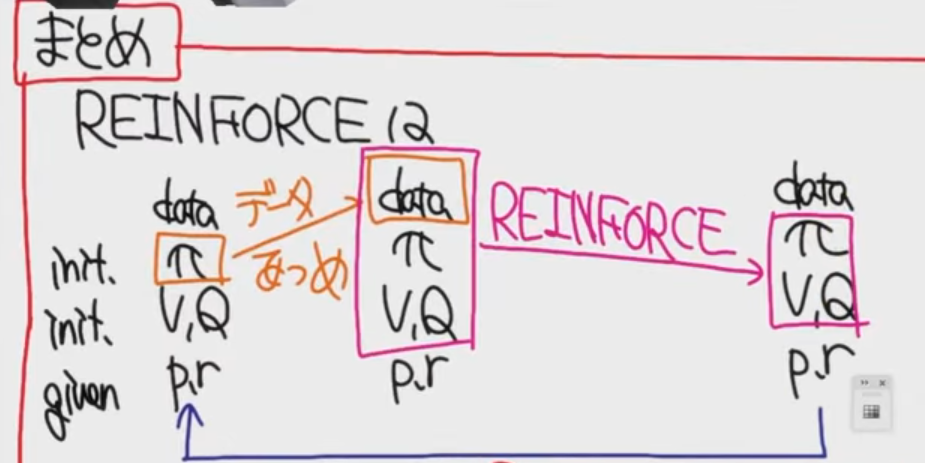
図に出てくる記号は、強化学習でよく使われる基本的な要素を表しています。

π（パイ）

方策（policy）のこと。
状態

s_t

を見て、どの行動

a_t

をとるかを決める確率分布。
Reinforceでは、この

\pi(a|s)

のパラメータを勾配法で更新する。

V（バリュー）

価値関数（state value function）。
ある状態

s

からスタートしたときに、将来得られる報酬の期待値。
式で書くと：

V^\pi(s) = \mathbb{E}\Big[ \sum_{t=0}^\infty \gamma^t r_t \,\big|\, s_0=s, \pi \Big]

Q（キュー）

行動価値関数（action value function）。
状態

s

で行動

a

を選んだ場合に、将来得られる報酬の期待値。
式で書くと：

Q^\pi(s,a) = \mathbb{E}\Big[ \sum_{t=0}^\infty \gamma^t r_t \,\big|\, s_0=s, a_0=a, \pi \Big]

p（ピー）

環境の遷移確率。
「状態

s

で行動

a

を取ったら、次に状態

s'

に遷移する確率」を表す。
式で書くと：

p(s'|s,a)

r（アール）

報酬（reward）。
行動を取った直後に得られるスカラー値。
学習の目的は、これをできるだけ大きく積み上げるように方策

\pi

を改善すること。

要するに、

$\pi$
$V, Q$
$p, r$

VとQの違いを教えて下さい。

良い質問です。VとQはどちらも「将来の報酬の期待値」を表しますが、見る単位が違うのがポイントです。

V（価値関数, Value Function）

「状態の価値」を表す
状態 $s$
数式：

V^\pi(s) = \mathbb{E}\Big[\sum_{t=0}^{\infty}\gamma^t r_t \,\big|\, s_0 = s, \pi \Big]

例：迷路で「スタート地点にいるとき、この後うまく進んでゴールできそうか？」を評価

Q（行動価値関数, Action Value Function）

「状態＋行動の価値」を表す
状態 $s$
数式：

Q^\pi(s,a) = \mathbb{E}\Big[\sum_{t=0}^{\infty}\gamma^t r_t \,\big|\, s_0 = s, a_0 = a, \pi \Big]

例：迷路で「スタート地点から右に進んだ場合に、最終的にゴールできそうか？」を評価

違いを直感で言うと

Vは「この場所そのものがどれくらい良いか」
Qは「この場所でこの行動を取ったらどれくらい良いか」

もしご希望なら、この違いを「簡単な迷路の図」を使って具体的に数値例で示すこともできますが、やってみますか？

お願いします。

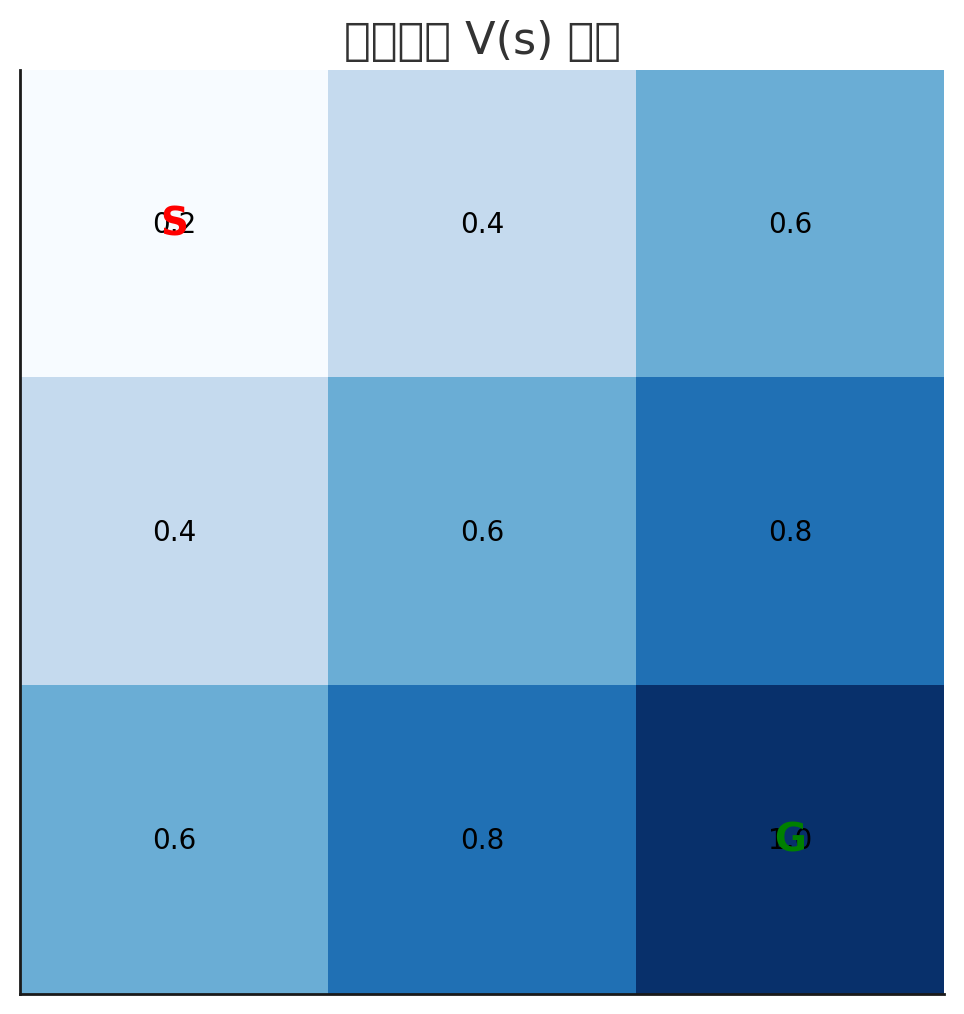
この図は、3×3の簡単な迷路での 状態価値 V(s) の例です。

ゴール（G）に近づくほど $V(s)$
スタート（S=左上）の $V(s)=0.2$

一方で、行動価値 Q(s,a) は「状態＋行動」の評価です。
例えばスタート地点 S での Q 値は次のように設定しました：

右に進む → $Q(s,a)=0.4$
下に進む → $Q(s,a)=0.4$
左に進む → $Q(s,a)=0.0$
上に進む → $Q(s,a)=0.0$

まとめると：

V(s) = その場所にいる「価値」
Q(s,a) = その場所で「特定の行動をとった場合の価値」

という違いになります。

ご希望なら、この例を「数式の形（VとQの関係式）」に落とし込んで整理することもできますが、続けますか？

続けて下さい

では、先ほどの迷路例を使って、数式でVとQの関係を整理します。

1. Q関数の定義

行動価値関数

Q^\pi(s,a)

は、状態

s

で行動

a

を選んだときの将来報酬の期待値です。

Q^\pi(s,a) = \mathbb{E}\Big[ r(s,a) + \gamma V^\pi(s') \,\big|\, s, a \Big]

$r(s,a)$
$\gamma$
$s'$

2. V関数とQ関数の関係

状態価値関数

V^\pi(s)

は、その状態にいるとき、方策

\pi

に従って行動したときの期待値です。

V^\pi(s) = \mathbb{E}_{a \sim \pi(\cdot|s)} \big[ Q^\pi(s,a) \big]

つまり、

VはQの期待値
方策に従って「どの行動をどのくらいの確率で取るか」を平均したものがV

3. 迷路のスタート地点の例

スタート地点 S における Q 値を思い出します：

$Q(S,右) = 0.4$
$Q(S,下) = 0.4$
$Q(S,左) = 0.0$
$Q(S,上) = 0.0$

もし「右と下を半々の確率で選ぶ」方策なら：

V(S) = 0.5 \times Q(S,右) + 0.5 \times Q(S,下) = 0.5 \times 0.4 + 0.5 \times 0.4 = 0.4

このように、VはQの加重平均として計算できます。

まとめ

Qは「行動レベルの価値」
Vは「行動を選ぶ方策を平均した状態レベルの価値」
数式で両者は明確に結びついており、VはQの期待値になっている

ここまでで「VとQの違い」と「数式でのつながり」を説明しました。

REINFORCEとは、方策購買定理もどきをデータの平均値をつかって行えるもの、と、とりあえず理解。

「Actor-CriticでVとQがどう使われるか」に踏み込んで下さい。

承知しました。ここからは Actor-Critic 法 における V と Q の役割を整理して説明します。

1. Actor-Critic とは何か

Actor（方策担当）：方策 $\pi(a|s)$
Critic（批評担当）：状態や行動の「価値」を推定する。Actor の行動が良いか悪いかを評価する役。

Reinforce単独では「得られた報酬だけ」を使って更新するため分散が大きいが、Criticを導入することで安定性が向上する。

2. Critic が使うもの：VかQか

Criticは大きく分けて2種類あります。

(A) State-value critic（V関数を使う）

Critic は $V(s)$
Actor の更新には「アドバンテージ（advantage）」を使う：

A(s,a) = Q(s,a) - V(s)

これにより「平均より良い行動かどうか」を基準に学習できる。

(B) Action-value critic（Q関数を使う）

Critic が直接 $Q(s,a)$
Actor は「Q値の高い行動をより選びやすくなるように」方策を更新する。

3. 更新の仕組み（簡略化）

Actor のパラメータ

\theta

を更新するとき、Reinforceでは：

\theta \leftarrow \theta + \alpha \nabla_\theta \log \pi_\theta(a|s) \cdot G_t

（ここで

G_t

は将来報酬の合計）

Actor-Critic では Critic の推定を組み込んで：

\theta \leftarrow \theta + \alpha \nabla_\theta \log \pi_\theta(a|s) \cdot \big(r + \gamma V(s') - V(s)\big)

この

(r + \gamma V(s') - V(s))

が TD誤差（Temporal Difference Error） で、実際の報酬と価値予測のずれを表す。

4. 直感的イメージ

Actor：「じゃあ右に進んでみよう」
Critic：「その結果の報酬とVを比べると予測よりちょっと良かったから、右を選ぶ確率を上げた方がいいね」

これを繰り返すことで、

Critic は環境を正しく評価できるようになり、
Actor は評価を参考により良い行動を選べるようになる。

5. まとめ

Actor-Critic は Reinforceの改良版
Critic が V または Q を学習し、Actor の更新に「評価基準」として使う
この仕組みにより、Reinforceの「分散が大きくて不安定」という弱点を補う

上記の図を使った例でActor-Criticを説明できませんか？

良い視点です。では、先ほどの 3×3迷路（スタートS・ゴールG） の図を使って、Actor-Critic がどう働くかを例で説明します。

1. 迷路の状況

スタート地点：S（左上）
ゴール：G（右下、報酬=+1）
Actor（方策）：上下左右に動く確率を持っている
Critic（価値関数）：各マスの「価値 $V(s)$

2. スタート時点での行動選択

スタートS(状態)にいるとき、Actorは確率的に行動を選ぶ：

右に行く確率 0.25
下に行く確率 0.25
左/上に行く確率 0.25ずつ

このとき、Criticは「Sの価値は0.2」と予測しているとします（前回の図より）。

3. 実際に行動 → 報酬観測

例えば「右へ移動」した場合、

即時報酬 $r = 0$

（ゴールではないので0）
次の状態Sは $(0,1)$

4. Criticによる評価（TD誤差）

Criticは「予測と実際の差」を計算します：

\delta = r + \gamma V(s') - V(s)

ここで

\gamma=0.9

とすると、

\delta = 0 + 0.9 \times 0.4 - 0.2 = 0.16

→ 予測より「ちょっと良かった」と判断。

5. 更新の流れ

Criticの更新
「Sの価値予測を上方修正した方がよい」と学習する。
Actorの更新
「右に行く行動は予測より良かったので、その確率を上げるように」学習する。

6. 繰り返しの結果

この流れを何度も繰り返すことで：

Criticは「各マスの価値」を正しく近似できるようになる
Actorは「ゴールに近づく行動の確率」を徐々に高める
最終的に「スタートから右か下に進み、効率的にゴールする方策」が得られる

まとめ

図の $V(s)$
Q や TD誤差は「行動が平均より良かったか」を判断する材料
Actor はこの評価をもとに「良い行動を強化、悪い行動を抑制」する

もしご希望なら、この迷路をシミュレーションして、実際にActorの行動確率がどう変化するか をコードでお見せできますが、見てみますか？

2025年8月31日未分類

Posted by ebata