もしご希望なら、この迷路をシミュレーションして、実際にActorの行動確率がどう変化するか をコードでお見せできますが、見てみますか？ → お願いします。

2025年8月31日

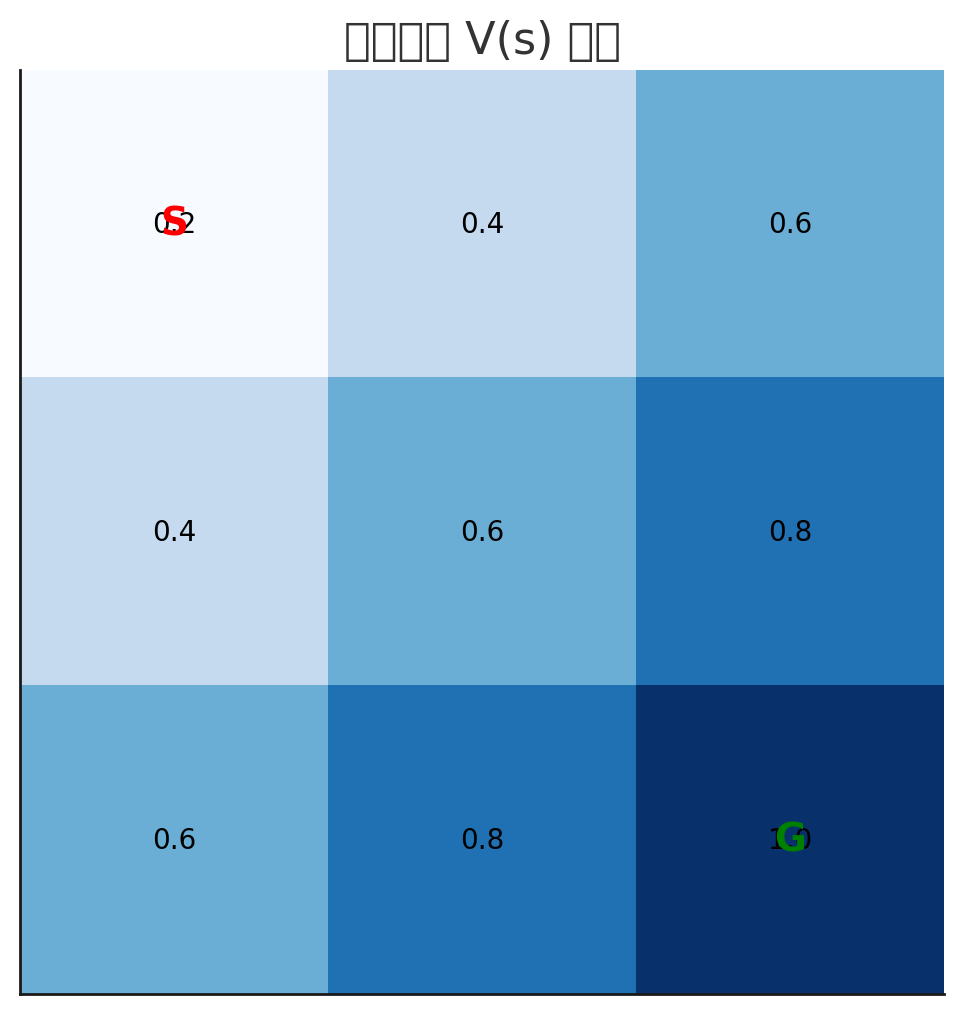
■迷路問題 : S(Start)から出発して、G(Goal)に至る迷路(？)
■お願いした事項: Go言語で作成をお願いします。

■プログラムで何をやっているか。

出てきたコードの各行の内容を全部質問して、コードの中に全部書き込みました。

時間はかかりましたが、ようやく分かってきました。

G:\home\ebata\actorcritic_maze3x3.go

package main

import (
	"fmt"
	"log"
	"math"
	"math/rand"
	"time"
)

type State struct{ r, c int }

const (
	rows, cols = 3, 3
	gamma      = 0.90 // 割引率
	alphaA     = 0.10 // Actor学習率
	alphaC     = 0.10 // Critic学習率
	episodes   = 4000 // 学習エピソード数
	maxSteps   = 50   // 1エピソード最大ステップ
	/*
		1. エピソード (episode) とは
		スタート地点からゴール or 強制終了まで の一連の試行を「1エピソード」と呼びます。
		このプログラムでは、S(0,0) から始めて、ゴール(G)に到着するか、maxSteps に達するまでが1エピソードです。
		episodes = 4000 は、この「試行」を4000回繰り返して学習を積み重ねる、という意味です。

		2. ステップ (step) とは
		エージェントが「行動を1回選んで、次状態に遷移し、報酬を得る」流れを1ステップと呼びます。
		maxSteps = 50 は、1エピソードの上限です。
		例えば、ゴールにたどり着けなかったとしても「50ステップ経ったら強制終了」して次のエピソードに移る、という仕組みです。
	*/

)

var (
	start = State{0, 0}
	goal  = State{2, 2}
	// 行動: 0=↑, 1=→, 2=↓, 3=←
	dirs = []State{{-1, 0}, {0, 1}, {1, 0}, {0, -1}}
)

// 迷路外・壁チェック（今回は外枠のみ）
func valid(s State) bool {
	return 0 <= s.r && s.r < rows && 0 <= s.c && s.c < cols
}

func step(s State, a int) (next State, r float64, done bool) {
	next = State{s.r + dirs[a].r, s.c + dirs[a].c}
	if !valid(next) {
		// 迷路外は元の場所にとどまる（報酬0）
		next = s
	}
	if next == goal {
		return next, 1.0, true // ゴール報酬
	}
	return next, 0.0, false
}

// ソフトマックス。数値安定化のため最大値を引く
func softmax(x []float64) []float64 {
	maxv := x[0]
	for _, v := range x {
		if v > maxv {
			maxv = v
		}
	}
	exp := make([]float64, len(x))
	var sum float64
	for i, v := range x {
		e := math.Exp(v - maxv)
		exp[i] = e
		sum += e
	}
	for i := range exp {
		exp[i] /= sum
	}
	return exp
}

// π(a|s) に従ってサンプル
func sample(probs []float64, rng *rand.Rand) int {
	u := rng.Float64()
	acc := 0.0
	for i, p := range probs {
		acc += p
		if u <= acc {
			return i
		}
	}
	return len(probs) - 1
}

func key(s State) int { return s.r*cols + s.c } // cols=3  keyはGivenか？

func main() {
	rng := rand.New(rand.NewSource(time.Now().UnixNano()))

	// Critic: V(s)
	V := make([]float64, rows*cols)

	// Actor: θ(s,a)（各状態で4行動のスコア）
	theta := make([][4]float64, rows*cols)

	// 学習ループ
	for ep := 0; ep < episodes; ep++ { // エピソード4000
		s := start
		for t := 0; t < maxSteps; t++ { // maxSteps=50
			if s == goal {
				break
			}

			// 方策 π(a|s) = softmax(θ(s,*))
			k := key(s) // 状態S = (r,c)を ｋ= r x cols + c で1次元に変換したもの

			scores := theta[k][:]
			/*
				theta は 「各状態ごとの4つの行動に対応するスコア（パラメータ）」 を保持する配列です。
				例えば状態が全部で9個（3×3迷路）なら、theta は [9][4]float64 型になります。
				1次元目 = 状態インデックス k
				2次元目 = 行動（↑→↓←の4つ）

				scores := theta[k][:] の意味
				theta[k] は、状態 k に対応する 4つの行動スコア（配列 [4]float64）です。
				[:] を付けることで、それを スライス（[]float64） として取り出しています。

				つまり、（↑→↓←の4つ）の行動スコアを取ってくる処理です。

			*/

			pi := softmax(scores)
			/*
				ここが Actor-Critic の Actor が「方策 π」を計算する部分 です。
				状態 s（インデックス k）における 行動スコア（4つ） が入っています。
				例：scores = [0.5, -0.2, 1.0, 0.0]

				2. softmax(scores) の処理
				ソフトマックス関数は、入力ベクトルを 確率分布 に変換します。これにより、行動スコアを「各行動を選ぶ確率」に変換できます。

				もし

				scores = [0.5, -0.2, 1.0, 0.0]
				pi := softmax(scores)

				とすると：
				exp(0.5) =1.65
				exp(-0.2)=0.82
				exp(1.0)=2.72
				exp(0.0)=1.00
				合計 = 1.65 + 0.82 + 2.72 + 1.00 = 6.19

				したがって確率は：
				π[0] = 1.65/6.19 = 0.27
				π[1] = 0.82/6.19 = 0.13
				π[2] = 2.72/6.19 = 0.44
				π[3] = 1.00/6.19 = 0.16
				となり、pi = [0.27, 0.13, 0.44, 0.16] となります。

				つまり、この状態で「下（3番目の行動）」を選ぶ確率が一番高い という方策が得られる。
			*/

			// 行動サンプル
			a := sample(pi, rng) // 「Actor が方策 π(a|s) に従って行動を選ぶ」処理
			/*
				もし pi = [0.1, 0.7, 0.2, 0.0] なら、
				10%の確率で行動0（↑）
				70%の確率で行動1（→）
				20%の確率で行動2（↓）
				0%の確率で行動3（←）
				が選ばれることになります。
			*/

			// 遷移
			s2, r, done := step(s, a)
			/*
				報酬 r は、環境に組み込まれた「設計者が定めたルール」によって与えられる数値です。
				- ある行動をしたときに「良いこと」が起きれば正の報酬
				- 「悪いこと」が起きれば負の報酬
				- 何も特別なことがなければ0
				報酬の設計は、人間（研究者・エンジニア）がタスクに合わせて 「何を良しとするか」 を決めているのです。

				今回のプログラムでは、ゴール以外はすべて報酬0 に設計されています。

				- ゴールに到着するまでは報酬が一切なく、ゴール時にだけ+1をもらえる
				- これは「スパース報酬（Sparse Reward）」と呼ばれる典型的な強化学習の難しい設定です
				- エージェントは「長い間0ばかりの報酬」を経験し、たまたまゴールに着けたときだけ「報酬1」を得る → そこから学習が始まる

				ちなみに、以下のような報酬にすることも可能です。
				- ゴールに近づいたら +0.1
				- 壁にぶつかったら -0.1
				- ゴールで +1
			*/

			// TD誤差 δ = r + γ V(s') - V(s)
			delta := r + gamma*V[key(s2)] - V[k]
			/*
				Q: 行動前後の状態関数値に、報酬値(行動関数値)を混在させているように見えますが、この理解で正しいですか

				まさに 「行動前後の状態価値に、報酬を加えた誤差（TD誤差）」 を計算しています。
				ご指摘の「混在させているように見える」というのは正しい理解です。

				V(s)：行動前の状態の予測価値
				r：その行動で得られた報酬（行動の良し悪しを直接反映）
				γ V(s')：次の状態の予測価値（将来の報酬を考慮）

				なぜ混在させるのか→これは Temporal Difference (TD) 学習 の基本です。
				- 強化学習は「報酬だけ」では学習が進まない（スパース報酬だと特に）。
				- そこで「次状態の価値」を推定値として使い、学習を効率化する。
				- 結果として「報酬（直接的な経験）」と「状態価値（推定値）」が混在する形になります。

				直感的なイメージ
				- 今の予測V(s) は「この場所は0.2くらいの価値」と言っている
				- でも実際に行動したら「報酬r=0」＋「次の状態の価値0.4×割引0.9 = 0.36」が得られた
				- すると「実際の方が良かった → 予測との差 δ=+0.16」
				- この δ を Actor と Critic の両方の更新に使う

				まとめ
				- ご指摘の通り、報酬 r（行動の直接的な結果）と状態価値 V（将来の見込み）を混ぜている
				- これは意図的で、「行動直後の経験」と「将来の予測」を組み合わせるのがTD学習の肝
				- この差分 δ が、学習の駆動力（Criticの改善、Actorの方策更新）になります
			*/

			// Critic更新
			V[k] += alphaC * delta // 	alphaC = 0.10   Critic学習率  Vは、状態価値関数を2次元で記載せずに、1次元にして管理している(プログラムを簡単にするため))
			/*
				Givenであった状態評価関数値に手を加える
			*/

			// Actor更新：∇θ log π(a|s) = onehot(a) - π
			for i := 0; i < 4; i++ {
				grad := -pi[i] // softmaxで作成された確率分布pi
				if i == a {    // aは4つの行動サンプルの中の1つ
					grad = 1.0 - pi[i]
				}
				theta[k][i] += alphaA * delta * grad // 	alphaA = 0.10 Actor学習率
			}
			/*
				Q: これは、行動評価関数を更新しているのだと思いますが、scoreの値(softmaxの前)と、piの値(softmaxの後)の値が混在して、混乱しています。

				ここで「行動スコア（softmax前）」と「行動確率分布 π（softmax後）」が混ざって見えるのは自然な感覚です。実際には役割が違います。まずそこを分けて整理します。

				1. 行動スコア（softmax前）
				theta[k][i] がその正体です。
				- これは 状態 s における各行動 a の「生の値（ロジット）」。
				- まだ確率ではありません。
				- 学習により増減して「相対的にどの行動が良いか」を表現する材料になります。

				例： theta[k] = [0.1, 0.9, -0.2, 0.0] この段階ではただの4つの数。

				2. 行動確率分布 π（softmax後）
				- pi := softmax(scores) で計算されるもの。
				- scores は theta[k][:] から取り出した 行動スコア。
				- softmaxを通すことで 確率分布（和=1） になる。
				- 実際に「次の行動をサンプルする」時に使われるのはこちら。
				- 上の例にsoftmaxを適用すると：	π=[0.23,0.52,0.11,0.14]
				- つまり、Actorの「行動方策 π(a|s)」になります。

				3. 混乱しやすいポイント
				- 更新するのは スコア（theta）
				- その更新量の計算に 確率（pi） が出てくる
				- この「スコアを確率に変換して行動を選び、その確率を使ってスコアを更新する」という循環構造が混乱の原因です。

				4. 整理すると
				- スコア（theta[k][i]) … 内部パラメータ、学習で直接更新される
				- 確率（pi[i]) … スコアをsoftmaxで正規化したもの、行動選択と勾配計算に使う
				- 更新式の中で「theta を更新するが、その更新量を決めるのに pi が出てくる」ので、同じループに両方の値が登場しているだけ、ということです。

				5. 「なぜ grad = onehot(a) - pi という形になるのかの説明をお願いします
				はい、ここは方策勾配法の核心のひとつです。
				grad = onehot(a) - pi がどこから出てくるのかを順を追って説明します。

				1. 方策勾配法の基本式

				Actorは「方策 π(a|s)」をパラメータ θ で表しています。
				更新式の基本は次です：
				∇θ​logπθ​(a∣s)
				この勾配に TD誤差 δ を掛けて 𝜃 を更新します。

				方策を softmax で定義しているので：
				π(a|s) = exp(θ(s,a)) / Σ exp(θ(s,a'))
				となります。これを用いると、勾配は次のように書けます：
				∇θ​logπθ​(a∣s) = ∇θ​(θ(s,a) - logΣ exp(θ(s,a')))
				= ∇​θ(s,a) - ∇θ​logΣ exp(θ(s,a'))
				= 1 - π(a|s)

				対数を取ると：
				log π(a|s) = θ(s,a) - log Σ exp(θ(s,a'))

				4. 勾配を計算
				この式を θ で微分すると:
				∇θ​logπθ​(a∣s) = ∇θ​(θ(s,a) - logΣ exp(θ(s,a')))
				= ∇​θ(s,a) - ∇θ​logΣ exp(θ(s,a'))
				= 1 - π(a|s)

				もし 𝑖 ≠ 𝑎 なら：（選ばれなかった行動）なら：
				∇θ​logπθ​(i∣s) = ∇θ​(θ(s,i) - logΣ exp(θ(s,a')))
				= ∇​θ(s,i) - ∇θ​logΣ exp(θ(s,a'))
				= 0 - π(i|s)
				= -π(i|s)

				上記をベクトル形式で書けば:
				∇θ​logπθ​(a∣s) = 1 - π(a|s)
				∇θ​logπθ​(i∣s) = -π(i|s)
				となり、コードの内容と一致します。

				grad = onehot(a) - pi は、softmax方策の勾配
				∇θ logπ(a∣s) を計算した結果そのもの

				これを使うことで、
				選んだ行動のスコアは強化され（確率↑）、
				選ばなかった行動のスコアは抑制される（確率↓）

				つまり、行動スコアを、行動スコアの確率値を乗算して、更新しつづけている、と理解すれば良いです。

			*/

			s = s2
			if done {
				break
			}
		}
	}

	// 学習結果の表示
	fmt.Println("学習後の方策 π(a|s)（↑,→,↓,← の順で確率を表示）")
	for r := 0; r < rows; r++ {
		for c := 0; c < cols; c++ {
			k := key(State{r, c})
			pi := softmax(theta[k][:])
			// 見やすいように丸め
			fmt.Printf("s=(%d,%d): [", r, c)
			for i, p := range pi {
				fmt.Printf("%.2f", p)
				if i < len(pi)-1 {
					fmt.Print(", ")
				}
			}
			fmt.Println("]")
		}
	}

	// 簡易検証：スタートから1エピソード実行
	fmt.Println("\nスタートから1回走らせた行動列（期待的には→や↓が増える）")
	trace := simulateOnce(start, theta)
	fmt.Println(trace)
}

func simulateOnce(s State, theta [][4]float64) []string {
	if len(theta) != rows*cols {
		log.Fatal("theta size mismatch")
	}
	actName := []string{"↑", "→", "↓", "←"}
	var seq []string
	for steps := 0; steps < maxSteps; steps++ {
		if s == goal {
			seq = append(seq, "G")
			break
		}
		pi := softmax(theta[key(s)][:])
		/*
			状態 s に対応する 行動スコア（theta） を取り出して softmax にかける。
			その結果、確率分布 π(a|s) を得る。
		*/

		a := argmax(pi)
		/*
			π の中で最も確率が高い行動を選択。
			学習の検証用なので「確率的サンプル」ではなく「最大確率行動（貪欲行動）」を選んでいます。
			つまり「学習済み方策がいま一番推している行動」を採用。

			(注)
			ここでは 学習済みの Actor（θ） だけを使って行動を選ぶ。
			Critic（V） は行動選択に登場しない。
		*/

		seq = append(seq, actName[a])
		/*
			actName は []string{"↑", "→", "↓", "←"} です。
			a は 0〜3 の整数（選んだ行動インデックス）。
			なので actName[a] は「その行動の記号（↑→↓←）」になります。
			append によって、シーケンス seq にその行動を追加していきます。
		*/

		ns, _, _ := step(s, a)
		s = ns
		/*
			step() は (次状態, 報酬, 終了フラグ) を返す関数です。
			ここでは戻り値のうち 次状態だけを ns に受け取り、報酬と終了フラグは _ で捨てています。
		*/

	}
	return seq
}

func argmax(x []float64) int {
	idx := 0
	best := x[0]
	for i := 1; i < len(x); i++ {
		if x[i] > best {
			best = x[i]
			idx = i
		}
	}
	return idx
}

出力結果:

学習後の方策 π(a|s)（↑,→,↓,← の順で確率を表示）

s=(0,0): [0.02, 0.73, 0.24, 0.02]

s=(0,1): [0.01, 0.04, 0.94, 0.01]

s=(0,2): [0.06, 0.06, 0.85, 0.04]

s=(1,0): [0.01, 0.94, 0.03, 0.02]

s=(1,1): [0.00, 0.95, 0.04, 0.01]

s=(1,2): [0.00, 0.01, 0.99, 0.00]

s=(2,0): [0.12, 0.65, 0.12, 0.11]

s=(2,1): [0.03, 0.91, 0.04, 0.02]

s=(2,2): [0.25, 0.25, 0.25, 0.25]

スタートから1回走らせた行動列（期待的には→や↓が増える）

[→ ↓ → ↓ G]