2022/11

Luxeritas テーマのアップデート方法

The target audiences of this primer are researchers and practitioners in the interdisciplinary fields of
transportation, who are specialized or interested in social science models, behavioral models, activitybased
travel demand models, lane use models, route choice models, human factors, and artificial
intelligence with applications in transportation.

こんな感じでemacsにコピペしたら、

  ← (見えないけど)半角のスペースが入っている。これで行末に" "'(半角スペース)が入る

としてから、

M-x replace-string C-q C-j (改行) (改行)

とすると、こうなる。

The target audiences of this primer are researchers and practitioners in the interdisciplinary fields of transportation, who are specialized or interested in social science models, behavioral models, activitybased travel demand models, lane use models, route choice models, human factors, and artificial intelligence with applications in transportation.

コマンド
タブ	C-q C-i
改行	C-q C-j

これから濫用すると思うので、メモ

以前、

円周内の一様乱数

から、乱数の生成を作ることができました。

現在、斜め45度くらいに述びた街の位置情報を乱数で作る為に、楕円周内の一様乱数を調べていたのですが、見つけられていません。

累積密度関数が一様になるように計算式を作れば良い、ということは分かったのですが、そんなの面倒くさくてやっていられません。

ふと思ったのですが、円周内の一様乱数ではθとr を使って、乱数を使っていて、この場合、r=sqrt(乱数)を使っているのだから、θの値に応じた新しいr'を作ってそのまま放り込んでやればいいのでは、と思いつきました。

面倒なので、x軸方向の長さは1.0として、y軸方向の長さをbとすれば、

x=cosθ 、 y=b sinθ となるので、r'= sqrt(x^2+y^2) に放り込むだけ、上記の円周内の一様乱数と同じやり方でできるんじゃないの、と考えて、エクセルで試しました。ここではb=0.5にしています。

結論:上手くいきませんでした。

もう面倒くさくなったので、r' に sqrt(0～1)の乱数を使って、x=cosθ 、 y=b sinθ に乗算するだめの「なんちゃって楕円内の一様乱数」 を作って対応しました。

こんな感じです。

// 住民の居住区を計算
		shita := 2.0 * 3.141592654 * rand.Float64()
		x := 0.03296 * math.Cos(shita)
		y := 0.01893 * math.Sin(shita)
		r := math.Sqrt(rand.Float64())
		rx := r * x
		ry := r * y
		//　45度回転 + 基本座標
		x_map := 1.0/math.Sqrt(2.0)*(rx-ry) + 131.46231887576513
		y_map := 1.0/math.Sqrt(2.0)*(rx+ry) + 34.171317284454766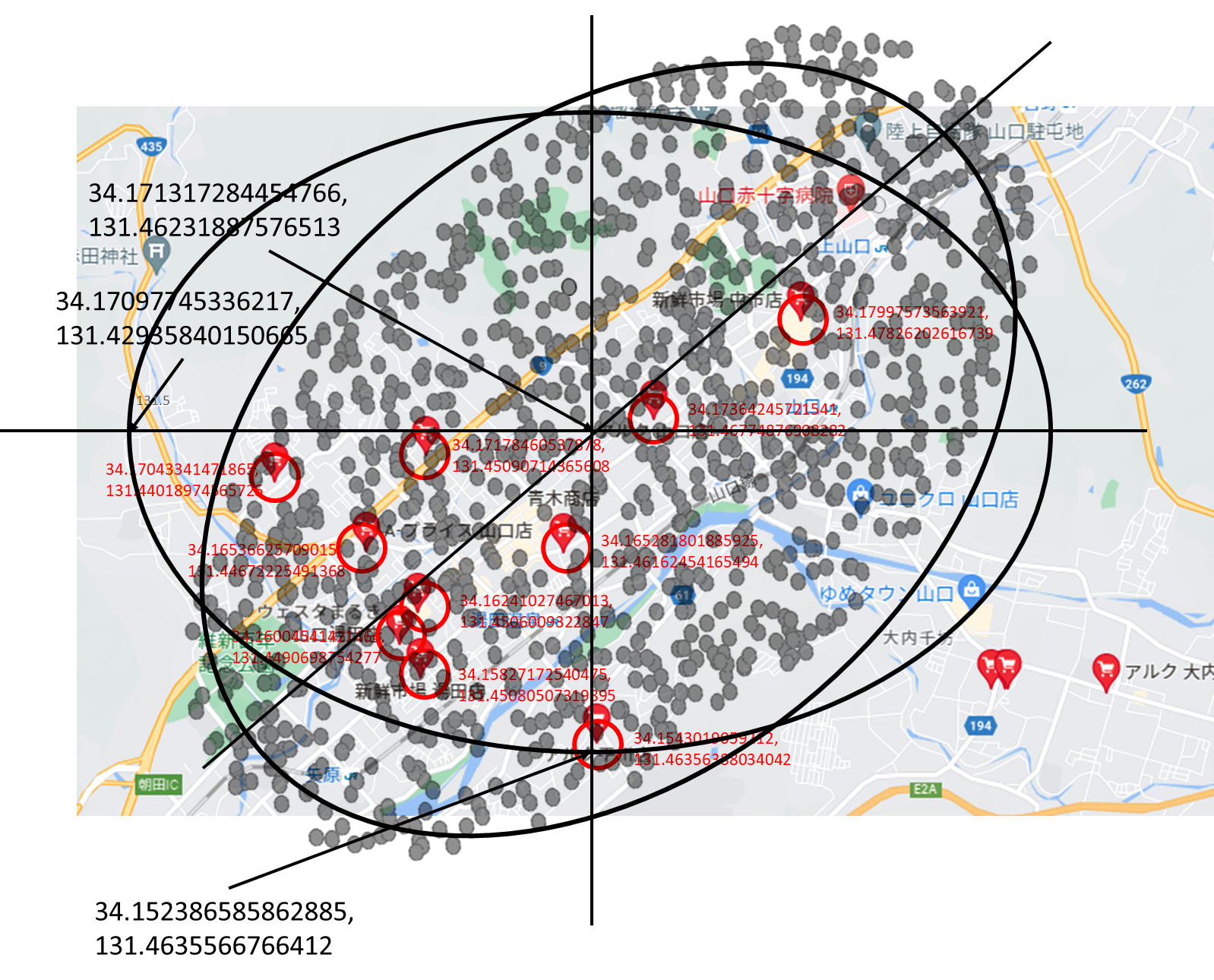

「ここは主戦場でなない」と腹を括って、逃げるのも、エンジニアには必須の技量です。