第三章を20回ほど読み直して、方式よりメソッドの理解に努めました。
資料5 『非集計ロジットのRプログラム例』のMNLモデルのサンプルコードを拡張したものを使っていたのですが、上手く動かなかったので、GO言語で作ってみました。
package main
import (
"encoding/csv"
"fmt"
"log"
"math"
"os"
"strconv"
"gonum.org/v1/gonum/mat"
"gonum.org/v1/gonum/optimize"
)
type Data struct {
所要時間 [6]float64
費用 [6]float64
利用可能性 [6]int
選択結果 int
}
func loadData(filename string) ([]Data, error) {
file, err := os.Open(filename)
if err != nil {
return nil, err
}
defer file.Close()
reader := csv.NewReader(file)
records, err := reader.ReadAll()
if err != nil {
return nil, err
}
var data []Data
for _, record := range records[1:] {
var d Data
for i := 0; i < 6; i++ {
d.所要時間[i], _ = strconv.ParseFloat(record[7+i], 64)
d.費用[i], _ = strconv.ParseFloat(record[13+i], 64)
d.利用可能性[i], _ = strconv.Atoi(record[1+i])
}
d.選択結果, _ = strconv.Atoi(record[0])
data = append(data, d)
}
return data, nil
}
func logLikelihood(x []float64, data []Data) float64 {
b := x[:6]
d1 := x[6]
f1 := x[7]
epsilon := 1e-10
LL := 0.0
for _, d := range data {
var v [6]float64
for i := 0; i < 6; i++ {
v[i] = b[i] + d1*(d.所要時間[i]/10) + f1*(d.費用[i]/10)
}
var vehicle [6]float64
var deno float64
for i := 0; i < 6; i++ {
if d.利用可能性[i] == 1 {
vehicle[i] = math.Exp(v[i])
deno += vehicle[i]
}
}
deno += epsilon
selected := d.選択結果 - 1
if selected >= 0 && selected < 6 {
P := vehicle[selected] / deno
LL += math.Log(P + epsilon)
}
}
return -LL
}
func initialLogLikelihood(data []Data) float64 {
numChoices := 6
initialProb := 1.0 / float64(numChoices)
L0 := float64(len(data)) * math.Log(initialProb)
return L0
}
func hessianMatrix(f func([]float64) float64, x []float64) *mat.Dense {
n := len(x)
hessian := mat.NewDense(n, n, nil)
epsilon := 1e-7
for i := 0; i < n; i++ {
for j := 0; j < n; j++ {
x1 := make([]float64, n)
x2 := make([]float64, n)
x3 := make([]float64, n)
x4 := make([]float64, n)
copy(x1, x)
copy(x2, x)
copy(x3, x)
copy(x4, x)
x1[i] += epsilon
x1[j] += epsilon
x2[i] += epsilon
x2[j] -= epsilon
x3[i] -= epsilon
x3[j] += epsilon
x4[i] -= epsilon
x4[j] -= epsilon
f1 := f(x1)
f2 := f(x2)
f3 := f(x3)
f4 := f(x4)
hessian.Set(i, j, (f1-f2-f3+f4)/(4*epsilon*epsilon))
}
}
return hessian
}
func main() {
data, err := loadData("transport_data.csv")
if err != nil {
log.Fatalf("データの読み込みに失敗しました: %v", err)
}
L0 := initialLogLikelihood(data)
fmt.Printf("初期尤度: %.4f\n", L0)
b0 := []float64{0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.01, 0.01}
problem := optimize.Problem{
Func: func(x []float64) float64 {
return logLikelihood(x, data)
},
}
result, err := optimize.Minimize(problem, b0, nil, nil)
if err != nil {
log.Fatalf("最適化に失敗しました: %v", err)
}
fmt.Println("パラメータ:", result.X)
fmt.Println("最終尤度:", -result.F)
hessian := hessianMatrix(problem.Func, result.X)
fmt.Println("ヘッセ行列:")
fmt.Printf("%v\n", mat.Formatted(hessian, mat.Prefix(" ")))
tValues := make([]float64, len(result.X))
for i := 0; i < len(result.X); i++ {
diag := hessian.At(i, i)
fmt.Println("diag:", diag)
if diag > 1e-5 {
tValues[i] = result.X[i] / math.Sqrt(diag)
} else {
tValues[i] = math.NaN()
}
}
fmt.Println("t値:", tValues)
LL := -result.F
likelihoodRatio := (L0 - LL) / L0
adjustedLikelihoodRatio := (L0 - (LL - float64(len(result.X)))) / L0
fmt.Printf("尤度比: %.4f\n", likelihoodRatio)
fmt.Printf("補正済み尤度比: %.4f\n", adjustedLikelihoodRatio)
}
データ(transport_data.csv)はこんな感じでした。
SELECT,TAXI,DRV,BIKE,BIC,WALK,BUS,TAXI_TIME,DRV_TIME,BIKE_TIME,BIC_TIME,WALK_TIME,BUS_TIME,TAXI_COST,DRV_COST,BIKE_COST,BIC_COST,WALK_COST,BUS_COST
2,1,1,1,1,1,1,480,180,300,360,1650,3360,563.22,318.16,6.05,2.42,1.21,210.00
6,1,1,1,1,1,1,180,150,240,300,1380,2760,500.00,317.02,5.67,2.27,1.13,210.00
5,1,1,1,1,1,1,90,60,120,150,720,900,500.00,309.33,3.11,1.24,0.62,210.00
2,1,1,1,1,1,1,450,120,180,210,840,2310,500.00,309.40,3.13,1.25,0.63,210.00
6,1,1,1,1,1,1,300,150,240,330,1470,870,500.00,317.06,5.69,2.27,1.14,210.00
6,1,1,1,1,1,1,330,180,270,330,1530,2040,500.00,317.06,5.69,2.27,1.14,210.00
6,1,1,1,1,1,1,330,210,330,420,1890,2340,593.18,319.66,6.55,2.62,1.31,210.00
6,1,1,1,1,1,1,300,180,330,420,1890,1410,593.18,319.66,6.55,2.62,1.31,210.00
6,1,1,1,1,1,1,450,120,210,270,1290,31770,500.00,315.31,5.10,2.04,1.02,210.00
6,1,1,1,1,1,1,450,150,240,270,1290,1920,500.00,315.31,5.10,2.04,1.02,210.00
6,1,1,1,1,1,1,90,60,90,90,390,24630,500.00,305.88,1.96,0.78,0.39,210.00
で計算結果は、10秒ほどで出てきました。
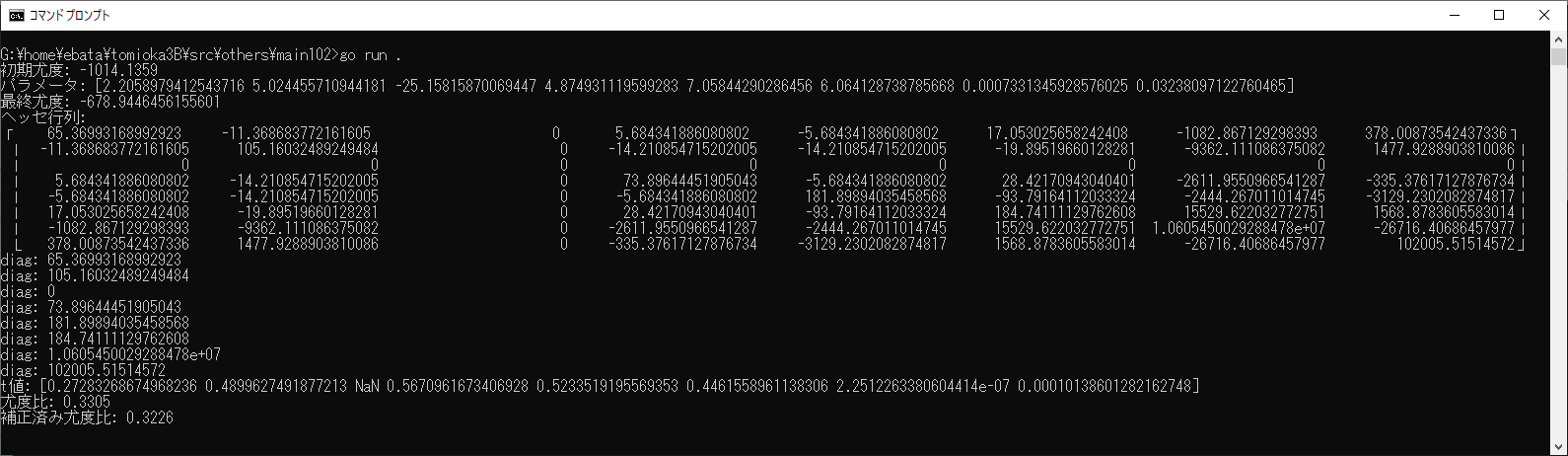
G:\home\ebata\tomioka3B\src\others\main102>go run .
初期尤度: -1014.1359
パラメータ: [2.2058979412543716 5.024455710944181 -25.15815870069447 4.874931119599283 7.05844290286456 6.064128738785668 0.0007331345928576025 0.03238097122760465]
最終尤度: -678.9446456155601
ヘッセ行列:
? 65.36993168992923 -11.368683772161605 0 5.684341886080802 -5.684341886080802 17.053025658242408 -1082.867129298393 378.00873542437336?
? -11.368683772161605 105.16032489249484 0 -14.210854715202005 -14.210854715202005 -19.89519660128281 -9362.111086375082 1477.9288903810086?
? 0 0 0 0 0 0 0 0?
? 5.684341886080802 -14.210854715202005 0 73.89644451905043 -5.684341886080802 28.42170943040401 -2611.9550966541287 -335.37617127876734?
? -5.684341886080802 -14.210854715202005 0 -5.684341886080802 181.89894035458568 -93.79164112033324 -2444.267011014745 -3129.2302082874817?
? 17.053025658242408 -19.89519660128281 0 28.42170943040401 -93.79164112033324 184.74111129762608 15529.622032772751 1568.8783605583014?
? -1082.867129298393 -9362.111086375082 0 -2611.9550966541287 -2444.267011014745 15529.622032772751 1.0605450029288478e+07 -26716.40686457977?
? 378.00873542437336 1477.9288903810086 0 -335.37617127876734 -3129.2302082874817 1568.8783605583014 -26716.40686457977 102005.51514572?
diag: 65.36993168992923
diag: 105.16032489249484
diag: 0
diag: 73.89644451905043
diag: 181.89894035458568
diag: 184.74111129762608
diag: 1.0605450029288478e+07
diag: 102005.51514572
t値: [0.27283268674968236 0.4899627491877213 NaN 0.5670961673406928 0.5233519195569353 0.4461558961138306 2.2512263380604414e-07 0.00010138601282162748]
尤度比: 0.3305
補正済み尤度比: 0.3226
ーーーーー
これを説明すると、
2.2058979412543716 → b_taxi
5.024455710944181 → ｂ_drv
-25.15815870069447 → b_bike
(以下省略)
となっており、
0.0007331345928576025 → d1
0.03238097122760465 → f1
効用関数は、次のようになります。
で、これをどう使うかは、以下の通り(ここからは分かった→シミュレータで使い倒すところ)
で、最後にパラメータの説明ですが、
となるようです。
ーーーーーーー
初期尤度: -1014.1359 と 最終尤度: -678.9446456155601の意味と意義は以下の通り。
======
今回の計算では、初期尤度: -1014.1359 に対して、最終尤度: -678.9446456155601が小さくなっているので、パラメータを使った方が良い、というのは理解できました。その場合、この
尤度比: 0.3305
および
補正済み尤度比: 0.3226
は何を表わしているか、は以下の通り。
======
負数値がついているので分かりにくいけど、
初期尤度: -1014.1359 → 最終尤度: -678.9446456155601 は、値が335も大きくなったということになります
======
尤度をもっとも簡単に説明する方法
つまるところ、偏ったコインを作る = パラメータをつけくわえる、という理解で良いようです。
=====
ところで、今回作成して頂いたモデルでマルチエージェントシミュレーションのエージェントに適用させたい場合、何を入力値として、エージェントの交通選択を選ぶことになるか？
"所要時間"と"費用"を入力値とすれば良い。
t値: [0.27283268674968236 0.4899627491877213 NaN 0.5670961673406928 0.5233519195569353 0.4461558961138306 2.2512263380604414e-07 0.00010138601282162748] のように値が小さいです
t値を大きくするためには、以下の3つの具体的なアプローチが考えられます。それぞれ、具体例を交えて説明します。
1. 標本数を増やす
標本数（サンプル数）を増やすと、t値が増加する可能性が高まります。これは、標本数が増えることで推定の**標準誤差が小さく**なり、結果としてt値が大きくなるためです。
- 例: ある多項ロジットモデルで、交通手段の選択確率を説明するための「時間」と「費用」の変数があるとします。最初のサンプル数が50の場合、時間の係数に対するt値が1.8で有意ではなかったとします。標本数を100に増やすと、標準誤差が小さくなり、同じ係数であってもt値が2.5になり、有意となる可能性が高まります。
2. 変数のスケールを調整する
変数のスケールを調整することで、標準誤差を減らしt値を大きくすることができます。特に、変数の分布が狭い範囲に集中している場合、その変数をスケール調整すると係数の推定がより安定します。
- 例: 収入に関するデータが1000円単位で表されているとします。この場合、係数の標準誤差が大きくなりやすいことがあります。これを1万円単位にスケール変換すると、収入の変動がモデルに対してより明確に影響し、標準誤差が小さくなることでt値が増える可能性があります。
3. 説明変数の分散を大きくする
説明変数の値が全体として似通っている場合（例えば、分散が小さい場合）、t値が小さくなりやすいです。このため、変数の分散を増やすようにデータを調整することも効果的です。可能であれば、サンプルに多様な値を含むようにデータを収集します。
- 例: 交通手段の選択モデルにおいて「通勤距離」を変数に入れたとします。もしすべてのサンプルがほぼ同じ距離（例えば、全員が2～3 kmの範囲）であれば、分散が少なくt値も小さくなります。データ収集の際に5～10 kmなどの多様な距離を持つサンプルを増やすことで、距離の変化に応じた係数の影響が明確になり、t値が大きくなることが期待できます。
これくさいなぁ。今回の移動距離は、高々1km以内だったからなぁ。終端距離まで入れると変わるかもしれん
---
これらの方法は、すべて統計的にt値を大きくするために役立ちますが、注意が必要です。無理にt値を大きくすることは、分析結果の解釈を歪める可能性もあるため、変数やデータの内容、意味を十分に理解した上で適用することが重要です。
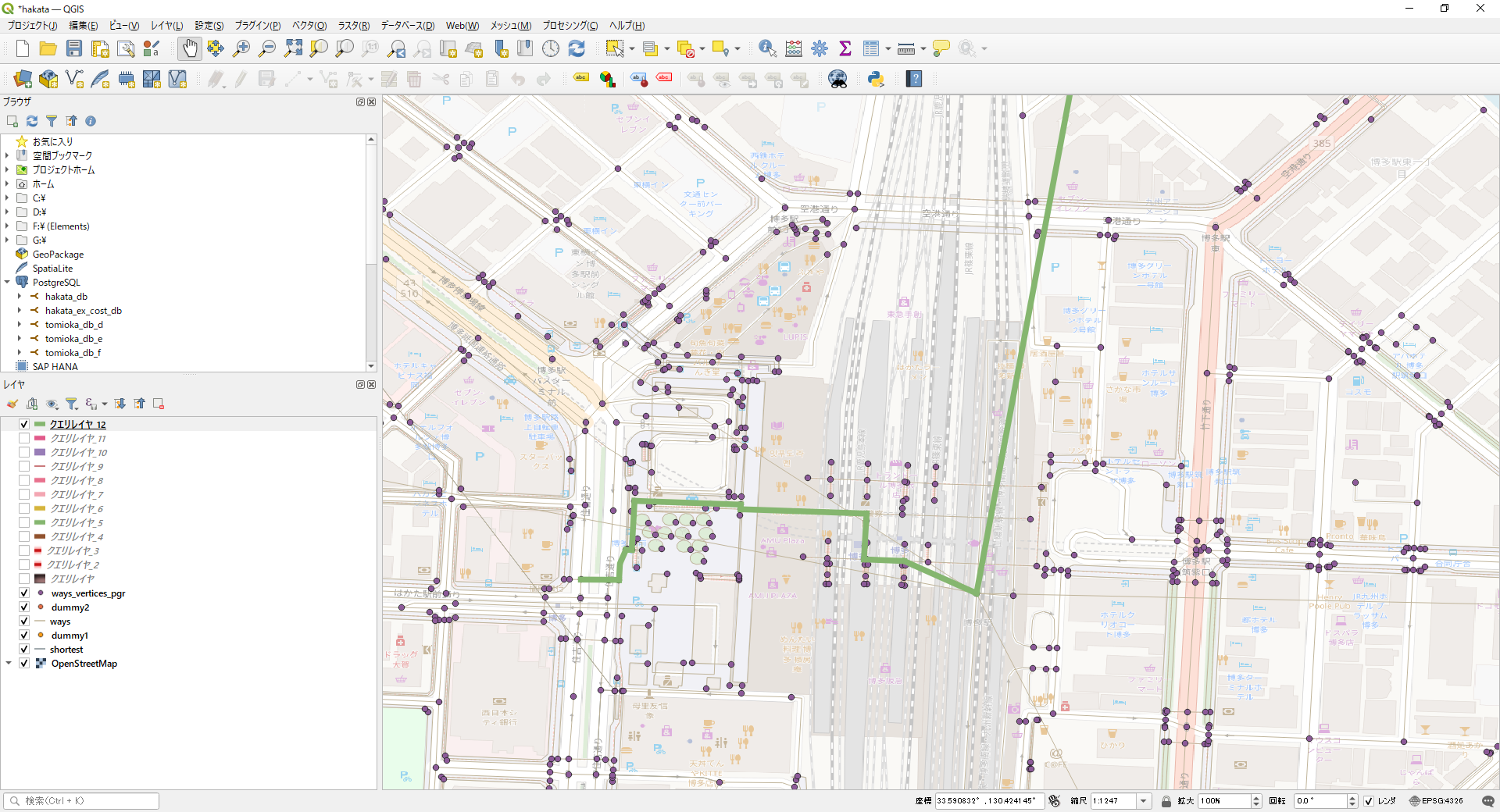
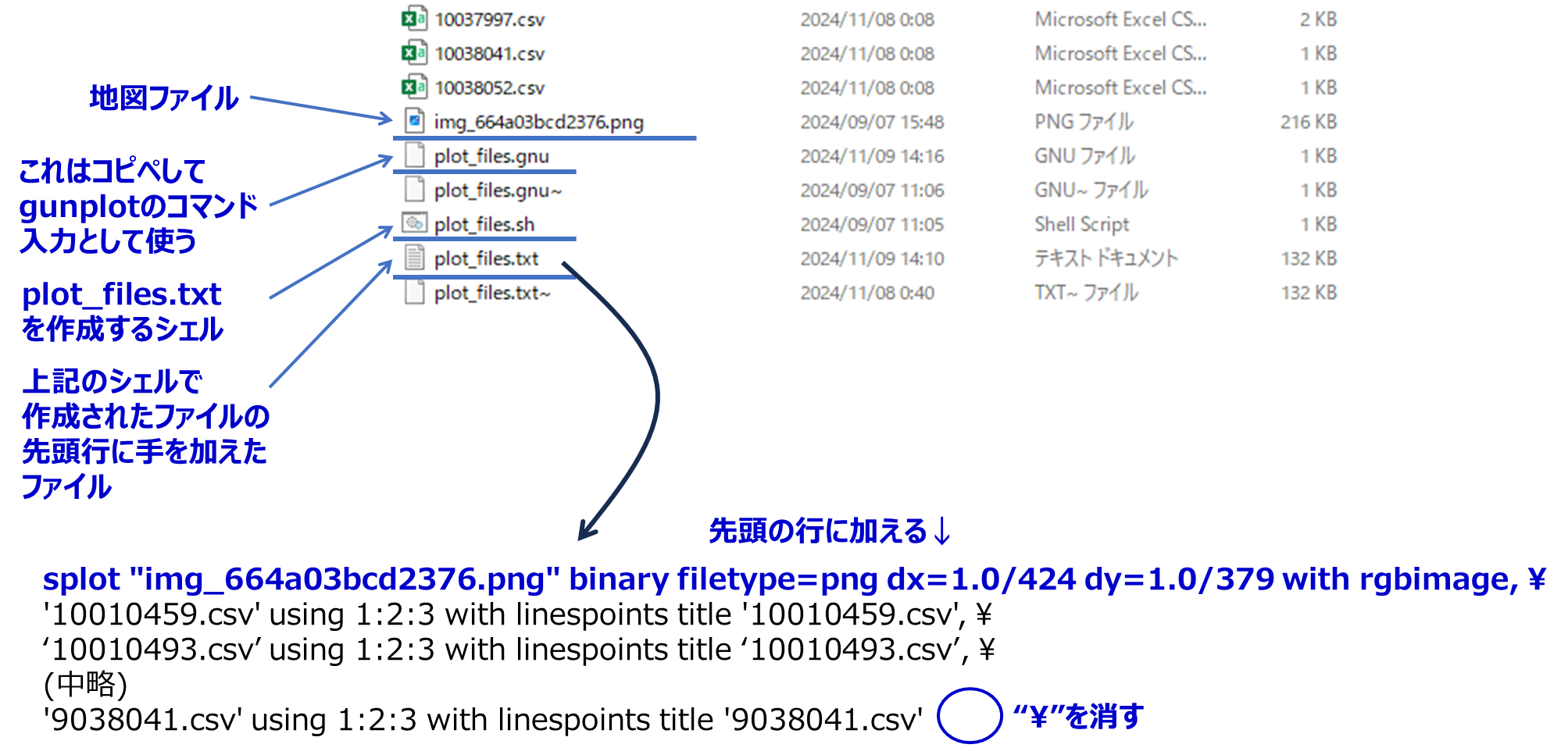
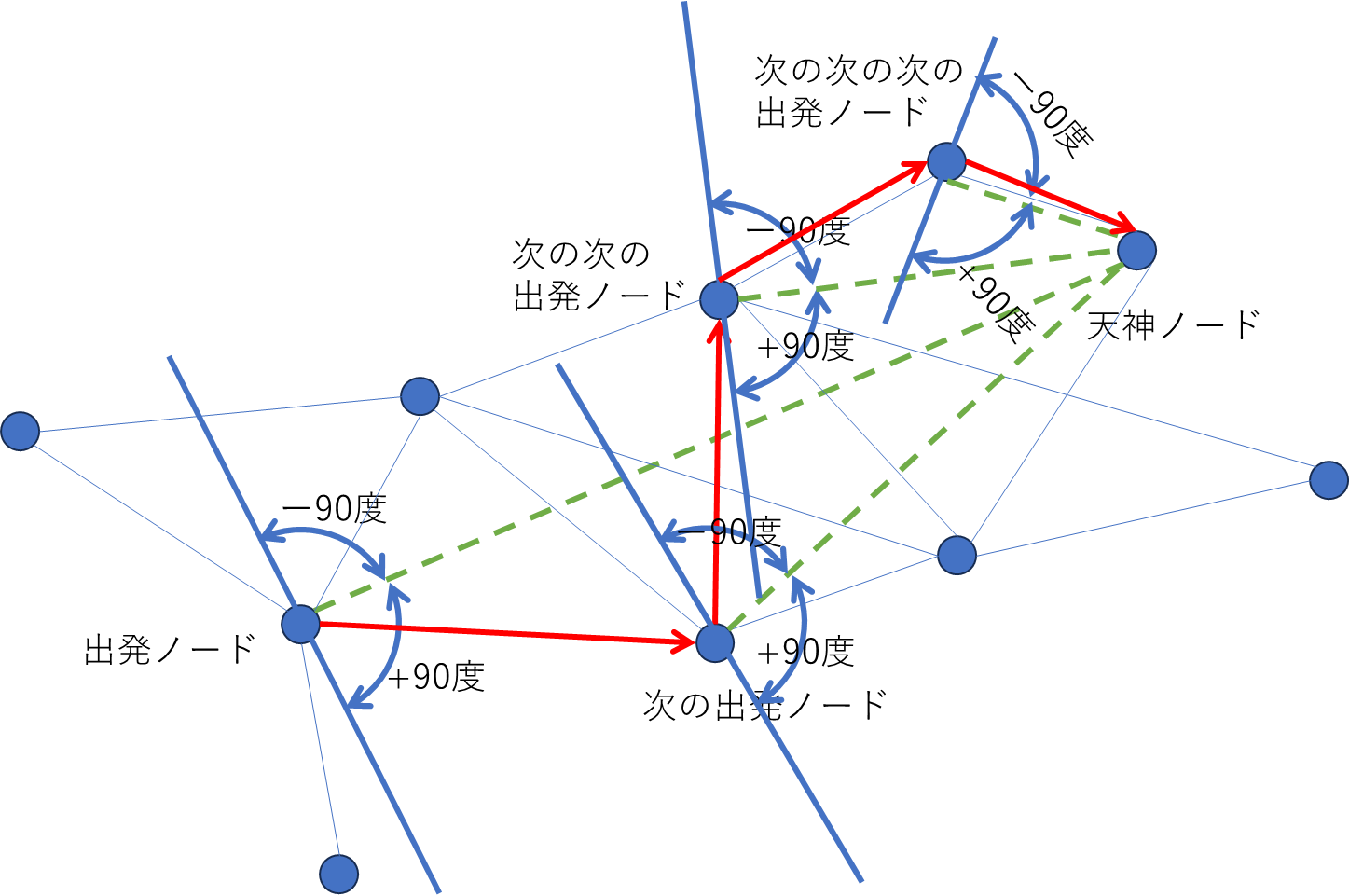
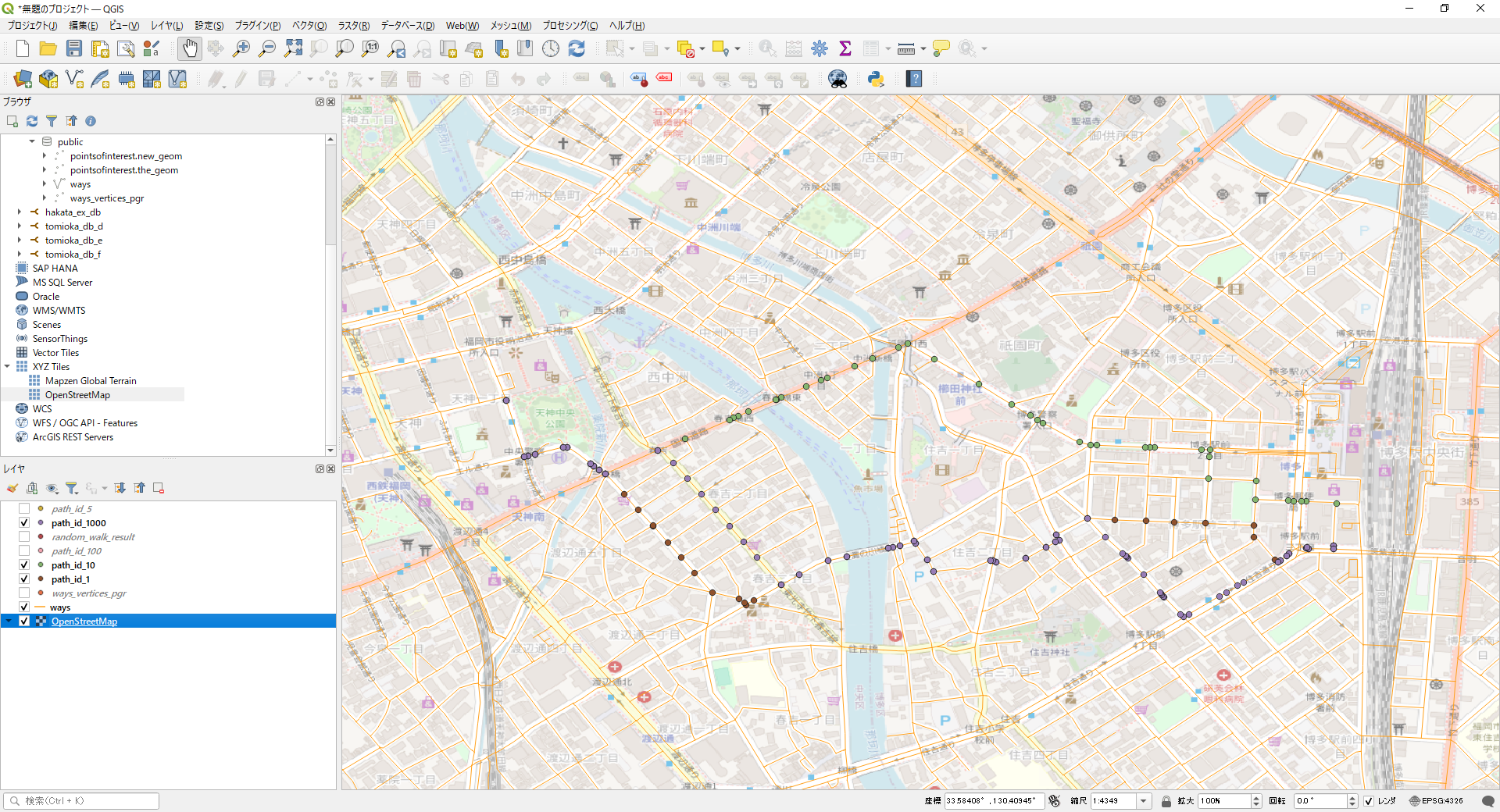まあ、ランダムウォークという感じではないですが、私たちが移動するときも、まあ、こんな感じだと思うので、とりあえずこれで進めようかなと思います。
